2017-03-17

Raspberry PiにZabbixサーバを建ててみた．

software make network

本題のとおり．
主にはこのサイトを参考にした．
Raspberry PiにZabbix 3.0をインストール
初代RasPiなので遅さを感じることはある．けれどもまぁいっかという感じ．使えていなくはないので．
他の機器の監視とかもSMNPとか使ってやってみたいなと思っている．温度だったりCPU，メモリとかの状態がすぐわかっていいかんじ．
インストール中に

configure: error: Not found Curl library

と言われたけども，

$ sudo apt-get install libcurl4-gnutls-dev

で治った（たしか）．
監視というのは安定的にサービスを提供する上でも，状態を知るという面でも大事なのでガシガシ使って行きたい．

References

2017-03-10

さくら野百貨店仙台店が破産した話．

study dialy

百貨店のビジネスモデル

この前私の住んでいる宮城県の仙台駅近くにある"さくら野百貨店"が店を閉じることになった．さくら野百貨店を運営していたマルシェという会社によれば，負債総額が31億円，約120人の従業員は解雇ということになるようだ．さくら野仙台店の売り上げはこの10年で半分程度に減少していたようで，駅前の競争に負けてしまったようだ．競争相手は駅前の店だけでなく，仙台港周辺や，泉，錦ケ丘にあるいわゆるアウトレットモールと呼ばれる大型のショッピング施設，また，長町や泉中央付近にあるショッピングモール等との競争もあるものだと思われる．特にここ10年ではアウトレットモールが立て続けにオープンしていたと思う．そのような側面もあるのだろう．近年入ったH&M，上階にあるムラサキスポーツやBOOK-OFFなどによる利用客の増加を見込んだそうだが，百貨店独自の高級感，ブランド感という面では裏目に出てしまったようだ．私が知る限りさくら野になる前はビブレという名前で営業していたことを覚えている．長く続く百貨店が幕を降ろすことになったという衝撃はなかなか大きいものだ．

百貨店離れ

やっぱりこれはあると思う．いわゆる百貨店と呼ばれるところに行く必要がなくなってきた．ネット販売もあれば，専門店が直接街にショップを出したり，アウトレットモール的なところに出したりしている．百貨店に行く機会も以前と比べたら格段に減ったのではないだろうか．

百貨店のしくみ

百貨店ってどういう風に利益を出しているのかわからなかったので調べて見た．普通のショッピングモールとかと違うのだろうか？ショッピングセンターとの違いは？という疑問が湧いた．

仕入れの仕組み

委託仕入と消化仕入両方とも，売れたぶんだけを百貨店側が仕入れたことにする仕組み．商品が売れると，その売上高の一部を仕入れ代金としてサプライヤー（ブランド店）に支払う． 2つの違いは在庫が誰のものになるからしい．消化仕入なら，在庫はサプライヤーのもの，つまりそのブランド店などの専門店のものとなる．委託仕入なら，その百貨店のものとなる．そしてこの場合，売れ残ったらサプライヤーに返品という形をとる．

ショッピングセンターとの違いは何なの

ショッピングセンターは上に述べたような百貨店を仲介しているような商品の売買は行われない．ショッピングセンター内にそれぞれのショップが賃貸借契約を結ぶ．これはショッピングセンターのこの区画を貸してもらって営業させてくださいというもの．要するに土地を借りたり部屋を借りたりするのと同様だ．商品が売れようが売れまいが，ショッピングセンター側は関係がない．それぞれのショップが商品を売ったり，従業員を雇って，売り上げはすべてショップのものとなる．その代わり，ショッピングセンターにショップを持つとなると，出店保証金等の初期コストがかかる，反対に百貨店は純粋な売り上げの一部を百貨店側に支払っている代わりに，出店保証金などはかからず，ショップの内装なども百貨店との協議によって負担割合が決まったりするそうだ．

で？

百貨店が収入を得るには，入っているショップの売り上げというものがとても大事になってくるということですね．ショップの売り上げがないことには百貨店側の利益は存在しないわけです．もちろんショップの売り上げが減ることによるショップ自体への影響ありますが，百貨店と共同で商品を売っているようなものでもあるので，ショップだけの影響ということにはなりません．反対にショッピングセンターの場合，入っている店舗の売り上げがどうであろうが，ショッピングセンター側はショップとの賃貸借契約に基づき，一定の収入を得ることができることになります．なのでこの場合，ショップの売り上げが減れば，ショップ自体の経営が難しくなり，最終的にはそのショッピングセンターから撤退するなどといった措置を，ショップ側が取るということになります．

総じて，ショップから見ると百貨店は店舗を出しやすいが，売り上げの一部を百貨店に支払わなくてはならない，百貨店から見ると，ショップの誘致等はしやすく，百貨店の売り場の雰囲気づくりや，百貨店ブランドを形成しやすくなるが，ショップの売り上げがないと百貨店は生きていけない．
また，ショッピングセンターは，ショップの売り上げに左右されることなく常に一定の賃貸借料をもらえるが，ショップが入ってくれないことには収入がない，ショップとしては，ショッピングセンターに比較的初期投資にコストがかかるが，売り上げはすべて自分のショップのものとなる．
ということになると思います．

References

百貨店のビジネスモデルを探れ
 仙台駅前「さくら野百貨店」が破産　駅前競争に屈す
 J-Net21 ビジネスQ&A
現代流通の仕組み

2017-02-25

おもちゃを分解する子供

dialy make

おもちゃを分解する子供

もし自分の子供が家のおもちゃや家電を分解する子供ならどうだろう．

私ならルールを決めてどしどし分解させたいと思う．おもちゃや家電を分解したいという欲求は知らないことを知りたいと思う欲求ではないでしょうか．それは，知らないことに対して疑問を持つこと．少しでも知りたいと思うこと．そういう感性というものは，大切にしたいと思う．

ルールを決めると述べたが，ルールというのは例えば次のようなもの．

分解したものは，かならず元に戻す．元の形，元の機能に戻す．
分解する前と分解して再結合したときに，親のチェックを受ける．

とか．簡単なものだ． 1つ目のルールは，分解するにあたって，その分解されるものの機能を失ったりすると，家庭に迷惑がかかるということを説明して学ばせる．また，元の状態に戻すにあたって，どうすれば元に戻せなくならないかを考えさせて学ばせる．つまるところ部品をきちんと管理させてなくさない，順番を覚えたり，書いておいたりさせて，再結合できなくなるリスクを減らすということを学ばせる．そして，「これ以上分解すると元に戻せなくなりそうだ．」と感じたら，そこで諦める（=自分のスキルを認めること）ことを学ばせる． 2つ目のルールはこれらの強制性を上げるような意味合いがある．

ものを分解することで得られることはとても大きいのではないのでしょうか．分解すること，知りたいと思うことを止めてはいけないと思う．ちゃんと決まりを決めればそれはすごくよい教材になる．そんなことを思っています．

もちろんやっていくうちに元に戻せないものも出てくることと思う．それはそれで，できなかったということをしっかり認めさせて，次はどうすればいいかを考えさせなければならない．私も小さいころに分解して元に戻せなくなることもしばしばあったものです…．

2017-02-25

最近のゾクゾクしたニュース

dialy make

最近のゾクゾクしたニュース

SpaceXのFalcon 9の打ち上げをライブストリーミングで見てしまった． SpaceX、Falcon 9ロケットの打ち上げ成功。見事な着地映像に夢を感じずにはいられない
普通のロケットの打ち上げと違うところは，SpaceXがUSの民間企業であることと，このロケットの1st stageは垂直離着陸型であることだ．すごいのは，もちろん1st stageの着陸である．見ていない人は一度は見て欲しい，動画サイトにアーカイブが上がっていると思う．発射後，地球の重力圏を抜けるために加速する任務を終えた1st stageは，そのまま海に落っこちるのではなく，指定された場所に戻ってくる．それも，垂直に着陸する．もちろんロケットなので，ロケットの下部にエンジンがついている．この状態で指定された場所まで誘導し，着陸する技術というのはものすごいことだ．姿勢の制御は主としてロケットの側面に取り付けられは可動式の羽のようなもので行なっているようだ．それに加え，メインエンジンと，数機のサブスラスタ（姿勢制御用）で行われているように見受けられる．ロケットという大きな制御対象をたったこれだけのアクチュエータだけで制御し，着陸して見せた．現代の制御技術，誘導技術の進化と，民間企業がここまでやってのけたことに対して，大きな衝撃を受けた． Space Xは幾度となく失敗している．Falcon 9も例外ではなく，以前にエンジンの燃焼試験中に爆発事故を起こしている．原因は液体ヘリウムタンクの破壊であったようだ．このように失敗を繰り返しても，大きなことをやり遂げたことには大きな意味があり，失敗してもめげずに歩みを続けることの大切さを見た．

初の自動運転レース「Roborace」クラッシュで幕を閉じる
これはF1もそろそろ自動運転になるんじゃないかと友人と話していたところにタイムリーな記事が飛んできたので載せてみる．自動運転技術は今や世界中の各社が開発を続ける技術である．すでに採石場のダンプ等の技術は実用化が行われている． F1は速度を競うレース，速度をあげようと思うとマシンのチューニング，それと技術を持ったドライバーが必要だ．しかし速度をあげようと思うと，どうしてもドライバーの命が問題になってくる．死亡事故が増えることは目に見えている．したがって，ドライバーのいないF1というのも面白そうだ．いくらでも高価なマシンを破壊できるわけではないが，人の人命に関わる倫理問題は回避できそうである．もとより，F1は人が運転するから面白いのだという意見も大変同意であるが．

総じて，現代の技術の進歩は本当に急速に進歩していることを見せつけられたということだ．

2017-02-08

R言語を使ってSmith Chartにプロットする

software hamradio

Smith Chartは美しい

高周波を扱っている人は一度は耳にしたことがあるだろう．このスミスチャートは，インピーダンスなどを特殊な関数によって描かれた平面上にプロットするものだ．スミスチャートを用いると，インピーダンスマッチングが容易になったり，一目でVSWRがどれくらいか分かったり，反射係数が分かったり，位相が何度ずれるか分かったり，Q値が分かったり…などなど，と，非常に便利なのだ．しかしながらこのスミスチャートの特殊性ゆえ，このグラフを美しく描画してくれるようなグラフソフトに出会うことが少ない．
そこで今回はおなじみのR言語を用いてこのスミスチャートを描いてみることにした．

さあ描こう．

色々と調べてみたら，Smith Chartの雛形を作製してくれている人を見つけた．
Plot Smith Chart in R - Stack Overflow
StackOverFlowは便利だ．このコードをありがたく頂戴してeditしてみる．

いろいろ試行錯誤した結果こんなものが生まれた．

#!/usr/bin/rscript --vanilla

#PDFに吐く場合
#filename='smith_chart.pdf'
#pdf(filename, 6, 6)

#入力するSパラメータファイルまでのパス
sp_filename = 'antenna.s2p'

# applies conformal map (z-1)/(z+1) to complex number z
cmap <- function(z) (z-1)/(z+1)

dd <- c(seq(-100, 100, 1), seq(-10, 10, 0.1), seq(-2, 2, 0.02))
dd <- round(dd, digits = 2) # fix roundoff errors
dd <- sort(unique(dd)) # remove duplicates

#こいつがSmithChartを描いてくれます．
smith_grid <- function (val, step) {
  # applies conformal map to lines having fixed real component
  r_grid <- outer(1i * dd[dd >= -val & dd <= val], seq(0, val, step), '+')
  r_grid <- cmap(r_grid)
  matlines(Re(r_grid), Im(r_grid), lwd = 0.5, col = 1, lty = 1)
  
  # applies conformal map to lines having fixed imaginary component
  x_grid <- outer(dd[dd >= 0 & dd <= val], 1i * seq(-val, val, step), '+')
  x_grid <- cmap(x_grid)
  matlines(Re(x_grid), Im(x_grid), lwd = 0.5, col = 1, lty = 1)
}

#観測データを読み込む，先頭が!の行はとばす
measure <- read.table(sp_filename,comment.char="!")
#必要な行だけ抜きだす．抜き出した後のデータはMagと角度(Deg)
measure <- measure[,c(2,3)]
#MagとDegから複素形式に変換．角度がradの場合は無論 /180*pi をしなくてよい．
cmp <- complex(mod=measure[,c(1)], arg=measure[,c(2)]/180*pi)

plot.new()
plot.window(c(-1, 1), c(-1, 1), asp = 1)

segments(-1, 0, 1, 0)
par(new=T)
theta <- seq(-pi, pi, length=100)
plot(cos(theta), sin(theta), type="l", asp=T, axes=FALSE, ann=FALSE)
smith_grid(50, 10)
smith_grid(10, 1)
smith_grid(3, 0.2)
smith_grid(0.6, 0.1)

#お好きな方を
matpoints(Re(cmp), Im(cmp), lwd = 1, col = 2, lty = 1,type = "o",pch=1, cex=0.2)
#matlines(Re(cmp), Im(cmp), lwd = 3, col = 2, lty = 1)

title(main="Smith Chart")

#dev.off()

実際にこれを使って適当なs2pファイルをプロットしてみた．
f:id:jp7fkf:20170208014016p:plain:w500
なかなかいい感じにプロットできていると思う． R言語はこういうプロットとかが自分の好きなようにできて便利だ．他のグラフソフトにはいろいろ制約が出てきたりしてしまったりするけどRは自分がコードを書きさえすればだいたい自由にできる．ただ書くのがめんどくさいけど．
統計解析とかの機能がついていてくれるから，それも利用してさらにプロットしたいなんという時には非常に便利なんじゃないかと思う．ソフトェアが1つで済むし．

ということで，きちんとR言語を用いてSmith Chartをプロットすることができました．
ちょっと今回のSmithChartには不満があって，右端側のところの等リアクタンス線とか描画されていない部分が気になったりしている．機会があれば直していきたいと思っている．

References

Keywords

Smith Chart
R Language
Plot
Graph
Draw

2017-02-04

私がサイエンスと技術が好きである理由

私がサイエンスと技術が好きである理由．

私はいわゆるサイエンスと技術が好きだ．たぶん．

子供の頃からサイエンスと技術には強い関心を持っていたと思っている．子ども百科の科学館と宇宙館を持っていたりサイエンスは好きだった．技術は，小学生に入るくらいの頃からパソコンを触り始めていて，それが楽しかった．Windows95．

ふと，なんで好きなのかを考えてみた．結論から言うと，「生きるため」と，「楽しむため」と言う結論に至った．

生きるためのサイエンス

サイエンスは，難しいことは抜きにして結局何をやっているかと言うと，身の回りのことを理解しようと努める学問ではないかと思う．
私たちは，この文章を見ている人は9割以上（？），地球に生まれてきた，と思う．この地球に生まれて，人間は生きようと努め続けてきた．生物としてこの地球に生まれ，後世にその種を保存しようとする．そのためにはまず，自分が生きねばならない．自分が生きるためには，まわりの環境のこと，生きる世界のことをよく知る必要があると思うし，知るべきであると思う．
もし，毒の含まれている木の実を知らなければ，それを食べて死ぬかもしれない．
もし，雷に打たれると死ぬと言うことを知らなければ，雷が周りに落ちている中で作業して死ぬかもしれない．
といった具合に（ちょっとわかりにくいが），人類の初期において生きるためにものを知るということはすなわちそれがサイエンスの原点なのではないかと思う．それが，多くの犠牲などを経て，現在におけるこの世界の知識が得られている．

近代におけるサイエンスは，例えば宇宙の銀河がどうたらとか，重力波がどうたらとか，恐竜の化石がどうとか，たぶん多くの人はそれを調べて何の役に立つんだとか思うこともなくはないのではないかと思う．それは，現代を生きる上では表面上必要になさそうに思えるけど，実は今後の私たちの未来に強く影響する可能性もないわけではないと思う．例えば恐竜がなぜ死んだのかがわかれば，私たちはもう一度その事象に直面する前に回避することができて，人類の滅亡の危機から逃れることができるかもしれない．そういうふうに考えると，サイエンスは生きることそのものなのではないかと思う．

私はたぶん生きたいと思っているし，今生きている世の中のことをもっと知りたいと思うことがよくある．だから多分私はサイエンスが好きだ．

サイエンスというのは，私たちに課せられた生きるための身の回りの世界をよく理解することかなと言う感じがする．

楽しむための技術

技術は本来は，我々の生活を豊かにするもので，すなわち生きることを楽しくするといえないだろうか．技術と一括りにしてしまうのも，楽しくするという大変広義な言葉で表現するのも難しいところだが，そう表現しても間違いではない気がする．技術といっても，ある方面では軍事目的であったり，人を殺すような技術も存在する．それは決して楽しくするようなものではない．ただ，技術は使い方によっては，人生をより楽しいものにする，人々の生活を便利にする，より有意義な人生を送れるとか，そういったことにも使えるであろう．

私が技術と接していて，ものごとを技術で解決できた時に私は喜びを感じることがある．そう言うふうに，目の前の人生における障壁であったりを，技術を使って簡単に乗り越えられるようにしたりする．それが技術なのかなと思う．
技術という言葉の指す範囲が本当に広いからうまくは言えないけど，言いたいことは伝わるだろうか…．

私は，人生を楽しくしたいと思っているし，他の人の人生も楽しくなったりすればいいなと思うことがある．だから多分私は技術が好きだ．

まとめ

総じて，たぶん私は人生を楽しく生きたいと思っているのかなという感じ．本当のところどうなのかは自分にもわからない．文章を書く能力があまりないので，全然何をいってるのかわからないかもしれないけど，やさしく捉えてみてほしい．

2017-01-25

はやぶさ2の地球スイングバイの見え方をFortranで計算していた話

software study

はやぶさ2の地球スイングバイについて

小惑星探査機「はやぶさ2」の地球スイングバイ実施結果について

「はやぶさ2」は、平成27（2015）年12月3日（木）の夕方から夜にかけて地球スイングバイを実施し、19時08分（日本時間）に地球に最接近、ハワイ諸島付近の太平洋上空約3,090kmを通過しました。

はやぶさ2は，近傍の小惑星「リュウグウ」ヘ向け，2014年12月3日に種子島宇宙センターからH-IIAロケット26号機で打ち上げられたものでした．打ち上げ後，しばらくは地球軌道と同じような公転軌道を回っていましたが，打ち上げから約1年後，地球の引力を利用した地球スイングバイが実施されています．これは，地球の引力により，はやぶさ2にさらなる加速をつけ，軌道も同時に変更するといったものです．イメージ的には，磁石があるとき，その磁石に対し，パチンコ玉などの鉄球をある角度，速度でうまく入射してやると，磁石の引力によりパチンコ玉の軌道が変化し，同時にパチンコ玉が加速すると言ったような感じです．これは磁石で遊んだことがある人ならわかるような気がします．イメージ的にはこんな感じ．
f:id:jp7fkf:20170125073659p:plain:w300
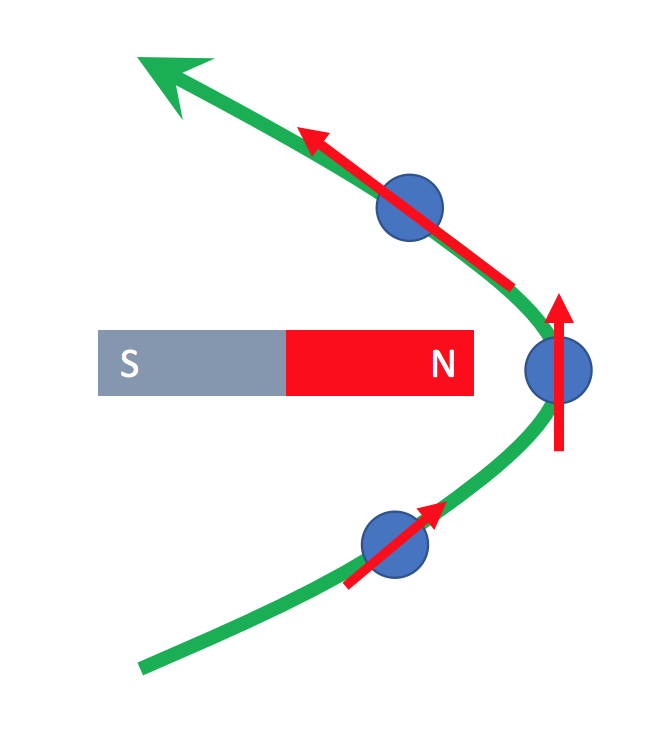
このしくみと全く同じようなことを，宇宙，地球という非常に大きなスケールで行うのが地球スイングバイです．この利点は，うまく入射軌道を調節してやれば，燃料をあまり消費せずに大きな加速度が得られ，速度が上がるということです．これは長い旅をするはやぶさ2にとっては非常に重要なことになります．

はやぶさ2の地球スイングバイを見る

実は，このときのはやぶさ2の地球スイングバイは，ちょうどハワイから日本の上空，ロシアにかけて地球に近づき，太平洋上空ではやぶさ2が地球に最接近するものでした．
ということは，そうです．日本からスイングバイが見れる可能性があったのです．そして，実際そのとき，複数の天文台ではやぶさ2が見れたという報告が上がっておりました．私も，はやぶさ2 スイングバイを見れるという情報を聞き，トライをしてみることを決めました．後から考えると，はやぶさ2は大型望遠鏡を持つ天文台のみでしか観測できなかったという無謀な挑戦だったのですが，実はその当時は，はやぶさが何等級の光として見えるか定かではなかったのです．太陽電池パドルの細かな向きによっても何等で見えるかが全く変わってくるためです．これははやぶさの姿勢をきちんと計算しても誤差要因によってかき消されてしまったり，日本のどこで見るかで全く違うことになり得るため，明るさは"見てみないとわからない"という状況でした．この希望にかけて私も観測を試みました．ミラーレスカメラを持ち，露光モードを長秒用の撮影にし，ずっとシャッターを切っていましたが，できた写真にははやぶさ2らしき軌跡は確認できませんでした．

はやぶさの軌道からどう見えるのか計算したくなった

観測に失敗した私は，実際自分の位置からはやぶさがどう見えるのか気になりました．地球の緯度，経度からはやぶさ2 スイングバイの見え方を計算してくれたサイトがありました．

2015年12月3日の「はやぶさ2」地球スイングバイの観測について（参考情報その1）
このサイトではこのような軌道が計算されて公表されています． f:id:jp7fkf:20170125073704j:plain （上記サイトより引用，ステラナビゲータ10／(株)アストロアーツ)

私はこれを参考に観測に挑戦していましたが，実はJAXAからはやぶさ2のスイングバイに関する軌道データが公表されています．
トピックス｢はやぶさ２｣の地球スイングバイについての情報を公開します！

ここの軌道データは3種類

データ１（UTF-8）：hy2_trj_EC_10min.txt
　　・黄道座標系
　　・11月3日から1月3日まで、10分間隔
　　・地球およびRyuguのデータ付き
データ２（UTF-8）：hy2_trj_EQ_1min.txt
　　・赤道座標系
　　・12月1日から12月5日まで、1分間隔
　　・「はやぶさ２」のみ
データ２（UTF-8）：hy2_trj_EQ_60min.txt
　　・赤道座標系
　　・11月3日から1月3日まで、60分間隔
　　・「はやぶさ２」のみ

この座標データから自分で軌道を計算して見ることにしました．

軌道を計算しよう

軌道を計算するのは，簡単といえば簡単です．ただの座標変換だからです． JAXAからは，ある座標系におけるはやぶさ2の位置と速度がxyz方向で示されています．したがってこの位置を座標変換し，自分のいる緯度，及び経度を参考に地球上での見え方にマッピングしてあげればよいのです．私は今回，データ2を用いることにしました．

このデータは，赤道座標系，これは地球中心J2000赤道面基準慣性座標系と呼ばれています．これは下記の富山大学の下記webサイトによると．
衛星航法システムにおける座標系

J2000.0（力学時2000年 1月1.5日，JD2451545.0)における平均赤道面，平均春分点の方向を基準（平均春分点の方向がｘ軸）とする慣性座標系であり、衛星運動方程式を積分して衛星の軌道を生成する座標系である．

とされています．つまり2000年 1月1.5日の天文の状況を考えてそれを基準にしますということです．
日々刻々と春分点や赤道面は地球の歳差運動などにより変化しうるので，これを日付も含めてfixしているということです．
この座標系から，地球の地上の座標に変換するだけです．
これをfortranで書いていましたので，今更ですが公開してみます．

PROGRAM haya2_swingby
  implicit none

  double precision coordinates(3),ecef_hy(3)
  integer year,month,day,hour, min,sec,i
  double precision, parameter :: longitude=140.872183d0, latitude=38.268737d0,height=0.0d0
  double precision, parameter :: a=6378137.0000d0, b=6356752.314250d0, omega_e=-7292115.467d-11
  double precision, parameter :: epoch_j2000=1449129600-946728000
  double precision, parameter :: Pi=3.141592653589793238
  double precision N_o,h_o,x_o,y_o,z_o
  double precision x,y,z
  double precision ro,azi,ele

  open(20, file="./hy2_trj_EQ_1min_mod.txt", status="old")

  DO i=0,959
    read(20, '(I4,5(1X,I2),3F20.1)'), year, month, day, hour, min, sec, coordinates(1), coordinates(2), coordinates(3)
    ecef_hy(1) = coordinates(1) * 1000 * cos(omega_e*(epoch_j2000+i*60)) + coordinates(2) &
    * 1000 * sin(omega_e*(epoch_j2000+i*60))
    ecef_hy(2) = coordinates(1) * 1000 * (-1)*sin(omega_e*(epoch_j2000+i*60)) + coordinates(2) &
    * 1000 * cos(omega_e*(epoch_j2000+i*60))
    ecef_hy(3) = coordinates(3) * 1000

    N_o=a**2/dsqrt(a**2*dcos(latitude*Pi/180)**2+b**2*dsin(latitude*Pi/180)**2)
    x_o=(N_o+height)*dcos(latitude*Pi/180)*dcos(longitude*Pi/180)
    y_o=(N_o+height)*dcos(latitude*Pi/180)*dsin(longitude*Pi/180)
    z_o=(b**2/a**2*N_o+height)*dsin(latitude*Pi/180)

    !print *, year, month, day, hour, min, sec, coordinates(1), coordinates(2), coordinates(3)
    x=ecef_hy(1)-x_o
    y=ecef_hy(2)-y_o
    z=ecef_hy(3)-z_o

    !print *,x,y,z

    ro = sqrt(x**2+y**2+z**2)
    azi = atan2(z,sqrt(x**2+y**2)) * 180 / Pi
    ele = (atan2(y,x)) * 180 / Pi

    print '(5I4,2F10.2,F15.1)',year,month,day,hour,min,azi, ele, ro/1000
    write(10,*) ele,azi

  END DO
  print *,epoch_j2000,4*3600+42*60+5
  OPEN(13,file="gnupdummy.plt")
    write(13,*) "reset"
    write(13,*) "set xrange [-180:180]"
    write(13,*) "set yrange [-90:90]"
    write(13,*) "plot 'fort.10' with points ps 0.5 pt 1"!with lines lw 1"
  CLOSE(13)
  call system("gnuplot gnupdummy.plt")
END PROGRAM haya2_swingby

緯度: 38度16分7.454秒(38.268737) 経度: 140度52分19.86秒(140.872183) は私の住んでいる宮城県の宮城県庁の座標です．これを使ってスイングバイ付近のデータで計算してみると f:id:jp7fkf:20170125073700p:plain このようなデータが得られます．
横軸は-180度から180度の水平角度，縦軸は-90度から90度の仰角を表しています．仰角がマイナスということは水平線の下にいるということです．
先ほどのwebサイトのデータを全く同じということにはなりませんでした．
これは，計算の方法で座標系の近似などを行ってしまったためだと思っています．
きちんと厳密に計算しているわけではないのです．
厳密にやりなおしてみたいと思いつつ今までやっていません．
もしかすると，完全に計算を間違えているのかもしれません．わかりません．
もし知見がある方がおられましたら是非ご指摘いただけると幸いです．

とはいえ，間違っているかもしれませんが，だいたいの傾向は同じものとなっています．
一応自分で参考程度の軌道情報を計算することができました．
当時，他の複数のwebサイトで検証をしていたのですが，この軌道に似ている形のものもあればそうでないものもあり，計算する人が使う手法によっても軌道の形は変わってしまうようです．
天文，宇宙の世界は細かい世界だと実感した瞬間でした．

JP7FKFの備忘録

ヒトは，忘れる生き物だから．

Raspberry PiにZabbixサーバを建ててみた．

References

さくら野百貨店仙台店が破産した話．

百貨店のビジネスモデル

百貨店離れ

百貨店のしくみ

仕入れの仕組み

ショッピングセンターとの違いは何なの

で？

References

おもちゃを分解する子供

おもちゃを分解する子供

最近のゾクゾクしたニュース

最近のゾクゾクしたニュース

R言語を使ってSmith Chartにプロットする

Smith Chartは美しい

さあ描こう．

References

Keywords

私がサイエンスと技術が好きである理由

生きるためのサイエンス

楽しむための技術

まとめ

はやぶさ2の地球スイングバイの見え方をFortranで計算していた話

はやぶさ2の地球スイングバイについて

はやぶさ2の地球スイングバイを見る

はやぶさの軌道からどう見えるのか計算したくなった

軌道を計算しよう

References