はやぶさ2の地球スイングバイの見え方をFortranで計算していた話
はやぶさ2の地球スイングバイについて
小惑星探査機「はやぶさ2」の地球スイングバイ実施結果について
「はやぶさ2」は、平成27(2015)年12月3日(木)の夕方から夜にかけて地球スイングバイを実施し、19時08分(日本時間)に地球に最接近、ハワイ諸島付近の太平洋上空約3,090kmを通過しました。
はやぶさ2は,近傍の小惑星「リュウグウ」ヘ向け,2014年12月3日に種子島宇宙センターからH-IIAロケット26号機で打ち上げられたものでした.
打ち上げ後,しばらくは地球軌道と同じような公転軌道を回っていましたが,打ち上げから約1年後,地球の引力を利用した地球スイングバイが実施されています.
これは,地球の引力により,はやぶさ2にさらなる加速をつけ,軌道も同時に変更するといったものです.
イメージ的には,磁石があるとき,その磁石に対し,パチンコ玉などの鉄球をある角度,速度でうまく入射してやると,磁石の引力によりパチンコ玉の軌道が変化し,同時にパチンコ玉が加速すると言ったような感じです.これは磁石で遊んだことがある人ならわかるような気がします.
イメージ的にはこんな感じ.
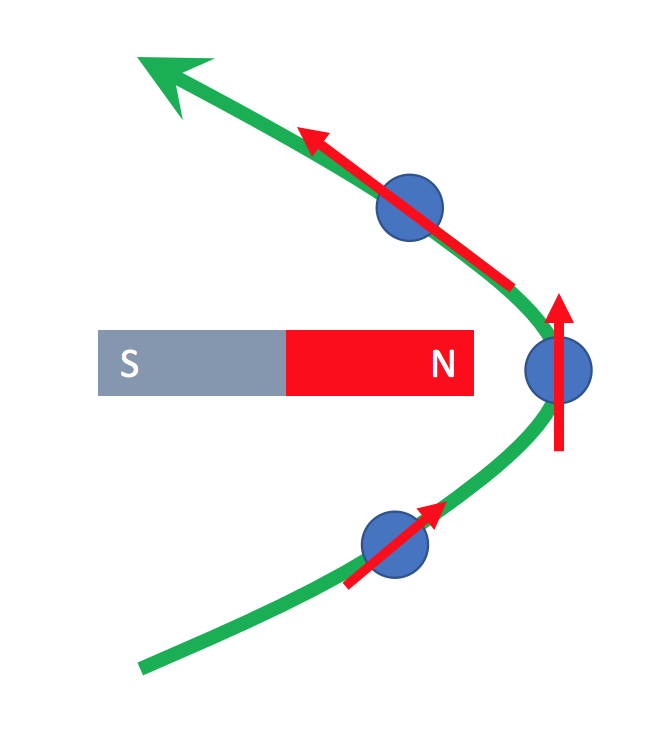
このしくみと全く同じようなことを,宇宙,地球という非常に大きなスケールで行うのが地球スイングバイです.
この利点は,うまく入射軌道を調節してやれば,燃料をあまり消費せずに大きな加速度が得られ,速度が上がるということです.
これは長い旅をするはやぶさ2にとっては非常に重要なことになります.
はやぶさ2の地球スイングバイを見る
実は,このときのはやぶさ2の地球スイングバイは,ちょうどハワイから日本の上空,ロシアにかけて地球に近づき,太平洋上空ではやぶさ2が地球に最接近するものでした.
ということは,そうです.日本からスイングバイが見れる可能性があったのです.
そして,実際そのとき,複数の天文台ではやぶさ2が見れたという報告が上がっておりました.
私も,はやぶさ2スイングバイを見れるという情報を聞き,トライをしてみることを決めました.
後から考えると,はやぶさ2は大型望遠鏡を持つ天文台のみでしか観測できなかったという無謀な挑戦だったのですが,
実はその当時は,はやぶさが何等級の光として見えるか定かではなかったのです.
太陽電池パドルの細かな向きによっても何等で見えるかが全く変わってくるためです.これははやぶさの姿勢をきちんと計算しても誤差要因によってかき消されてしまったり,日本のどこで見るかで全く違うことになり得るため,明るさは"見てみないとわからない"という状況でした.この希望にかけて私も観測を試みました.ミラーレスカメラを持ち,露光モードを長秒用の撮影にし,ずっとシャッターを切っていましたが,できた写真にははやぶさ2らしき軌跡は確認できませんでした.
はやぶさの軌道からどう見えるのか計算したくなった
観測に失敗した私は,実際自分の位置からはやぶさがどう見えるのか気になりました. 地球の緯度,経度からはやぶさ2スイングバイの見え方を計算してくれたサイトがありました.
2015年12月3日の「はやぶさ2」地球スイングバイの観測について(参考情報 その1)
このサイトではこのような軌道が計算されて公表されています.
 (上記サイトより引用,ステラナビゲータ10/(株)アストロアーツ)
(上記サイトより引用,ステラナビゲータ10/(株)アストロアーツ)
私はこれを参考に観測に挑戦していましたが,実はJAXAからはやぶさ2のスイングバイに関する軌道データが公表されています.
トピックス 「はやぶさ2」の地球スイングバイについての情報を公開します!
ここの軌道データは3種類
データ1(UTF-8):hy2_trj_EC_10min.txt
・黄道座標系
・11月3日から1月3日まで、10分間隔
・地球およびRyuguのデータ付き
データ2(UTF-8):hy2_trj_EQ_1min.txt
・赤道座標系
・12月1日から12月5日まで、1分間隔
・「はやぶさ2」のみ
データ2(UTF-8):hy2_trj_EQ_60min.txt
・赤道座標系
・11月3日から1月3日まで、60分間隔
・「はやぶさ2」のみ
この座標データから自分で軌道を計算して見ることにしました.
軌道を計算しよう
軌道を計算するのは,簡単といえば簡単です. ただの座標変換だからです. JAXAからは,ある座標系におけるはやぶさ2の位置と速度がxyz方向で示されています. したがってこの位置を座標変換し,自分のいる緯度,及び経度を参考に地球上での見え方にマッピングしてあげればよいのです. 私は今回,データ2を用いることにしました.
このデータは,赤道座標系,これは地球中心J2000赤道面基準慣性座標系と呼ばれています.
これは下記の富山大学の下記webサイトによると.
衛星航法システムにおける座標系
J2000.0(力学時2000年 1月1.5日,JD2451545.0)における 平均赤道面,平均春分点の方向を基準(平均春分点の方向がx軸) とする慣性座標系であり、衛星運動方程式を積分して衛星の軌道 を生成する座標系である.
とされています.つまり2000年 1月1.5日の天文の状況を考えてそれを基準にしますということです.
日々刻々と春分点や赤道面は地球の歳差運動などにより変化しうるので,これを日付も含めてfixしているということです.
この座標系から,地球の地上の座標に変換するだけです.
これをfortranで書いていましたので,今更ですが公開してみます.
PROGRAM haya2_swingby implicit none double precision coordinates(3),ecef_hy(3) integer year,month,day,hour, min,sec,i double precision, parameter :: longitude=140.872183d0, latitude=38.268737d0,height=0.0d0 double precision, parameter :: a=6378137.0000d0, b=6356752.314250d0, omega_e=-7292115.467d-11 double precision, parameter :: epoch_j2000=1449129600-946728000 double precision, parameter :: Pi=3.141592653589793238 double precision N_o,h_o,x_o,y_o,z_o double precision x,y,z double precision ro,azi,ele open(20, file="./hy2_trj_EQ_1min_mod.txt", status="old") DO i=0,959 read(20, '(I4,5(1X,I2),3F20.1)'), year, month, day, hour, min, sec, coordinates(1), coordinates(2), coordinates(3) ecef_hy(1) = coordinates(1) * 1000 * cos(omega_e*(epoch_j2000+i*60)) + coordinates(2) & * 1000 * sin(omega_e*(epoch_j2000+i*60)) ecef_hy(2) = coordinates(1) * 1000 * (-1)*sin(omega_e*(epoch_j2000+i*60)) + coordinates(2) & * 1000 * cos(omega_e*(epoch_j2000+i*60)) ecef_hy(3) = coordinates(3) * 1000 N_o=a**2/dsqrt(a**2*dcos(latitude*Pi/180)**2+b**2*dsin(latitude*Pi/180)**2) x_o=(N_o+height)*dcos(latitude*Pi/180)*dcos(longitude*Pi/180) y_o=(N_o+height)*dcos(latitude*Pi/180)*dsin(longitude*Pi/180) z_o=(b**2/a**2*N_o+height)*dsin(latitude*Pi/180) !print *, year, month, day, hour, min, sec, coordinates(1), coordinates(2), coordinates(3) x=ecef_hy(1)-x_o y=ecef_hy(2)-y_o z=ecef_hy(3)-z_o !print *,x,y,z ro = sqrt(x**2+y**2+z**2) azi = atan2(z,sqrt(x**2+y**2)) * 180 / Pi ele = (atan2(y,x)) * 180 / Pi print '(5I4,2F10.2,F15.1)',year,month,day,hour,min,azi, ele, ro/1000 write(10,*) ele,azi END DO print *,epoch_j2000,4*3600+42*60+5 OPEN(13,file="gnupdummy.plt") write(13,*) "reset" write(13,*) "set xrange [-180:180]" write(13,*) "set yrange [-90:90]" write(13,*) "plot 'fort.10' with points ps 0.5 pt 1"!with lines lw 1" CLOSE(13) call system("gnuplot gnupdummy.plt") END PROGRAM haya2_swingby
緯度: 38度16分7.454秒(38.268737) 経度: 140度52分19.86秒(140.872183)
は私の住んでいる宮城県の宮城県庁の座標です.これを使ってスイングバイ付近のデータで計算してみると
 このようなデータが得られます.
このようなデータが得られます.
横軸は-180度から180度の水平角度,縦軸は-90度から90度の仰角を表しています.
仰角がマイナスということは水平線の下にいるということです.
先ほどのwebサイトのデータを全く同じということにはなりませんでした.
これは,計算の方法で座標系の近似などを行ってしまったためだと思っています.
きちんと厳密に計算しているわけではないのです.
厳密にやりなおしてみたいと思いつつ今までやっていません.
もしかすると,完全に計算を間違えているのかもしれません.わかりません.
もし知見がある方がおられましたら是非ご指摘いただけると幸いです.
とはいえ,間違っているかもしれませんが,だいたいの傾向は同じものとなっています.
一応自分で参考程度の軌道情報を計算することができました.
当時,他の複数のwebサイトで検証をしていたのですが,この軌道に似ている形のものもあればそうでないものもあり,
計算する人が使う手法によっても軌道の形は変わってしまうようです.
天文,宇宙の世界は細かい世界だと実感した瞬間でした.